Seilkürzungen werden in AutoSTAGE Analysis über eine Ersatztemperaturlast modelliert. Über das Hookesche Gesetz wird eine Temperaturdifferenz errechnet, die das modellierte Seil um den angegebenen Betrag kürzt oder längt.
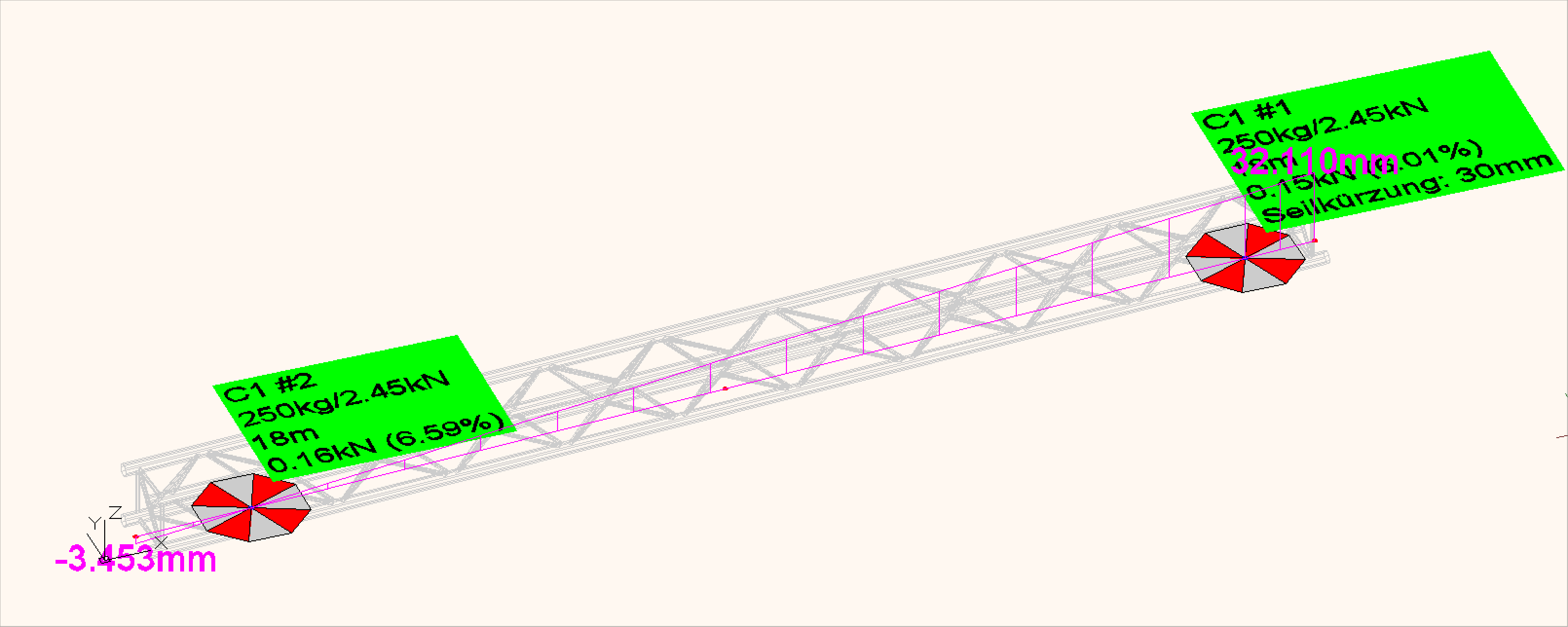
Die Seilkürzung von 30mm an rechten Auflager
ist deutlich in der Verformungsfigur zu erkennen.
Eine Seilkürzung kann für Drops, Hängepunkte und Motoren definiert werden. Über die Eigenschaft Seilkürzung kann der Betrag der Seilkürzung angegeben werden. Eine positive Seilkürzung steht für eine Kürzung, eine negative für eine Längung.
Mit Seilkürzungen kann man die Verteilung der Last auf die Hängepunkte deutlich anpassen. Denken Sie bei der Modellerstellung daran, dass die angegeben Werte für den Anzug auch in Praxis erreichen müssen um ihren Berechnungsergebnisse zu entsprechen. Das Arbeiten mit Seilkürzungen sollte dem erfahren Nutzer vorbehalten sein.
Tipp: Arbeiten Sie mit Seilkürzungen iterativ. Fangen Sie ohne Seilkürzungen an ihr System zu modellieren und fügen Sie nach und nach die gewünschten Seilkürzungen hinzu. Mit dem Befehl ASANRESETRETIGHT werden wieder alle Seilkürzungen zurückgesetzt.
Durch Seilkürzungen kann ein System schnell nicht mehr berechenbar sein. An einer Traverse an drei Seilen wird hier kurz die Problematik erläutert.
![]() Beispiel für Auswirkungen von Seilkürzungen
Beispiel für Auswirkungen von Seilkürzungen
Gegeben ist eine Traverse an drei Auflagern. Es wird nach Theorie II. Ordnung gerechnet, also können Seile ausfallen.
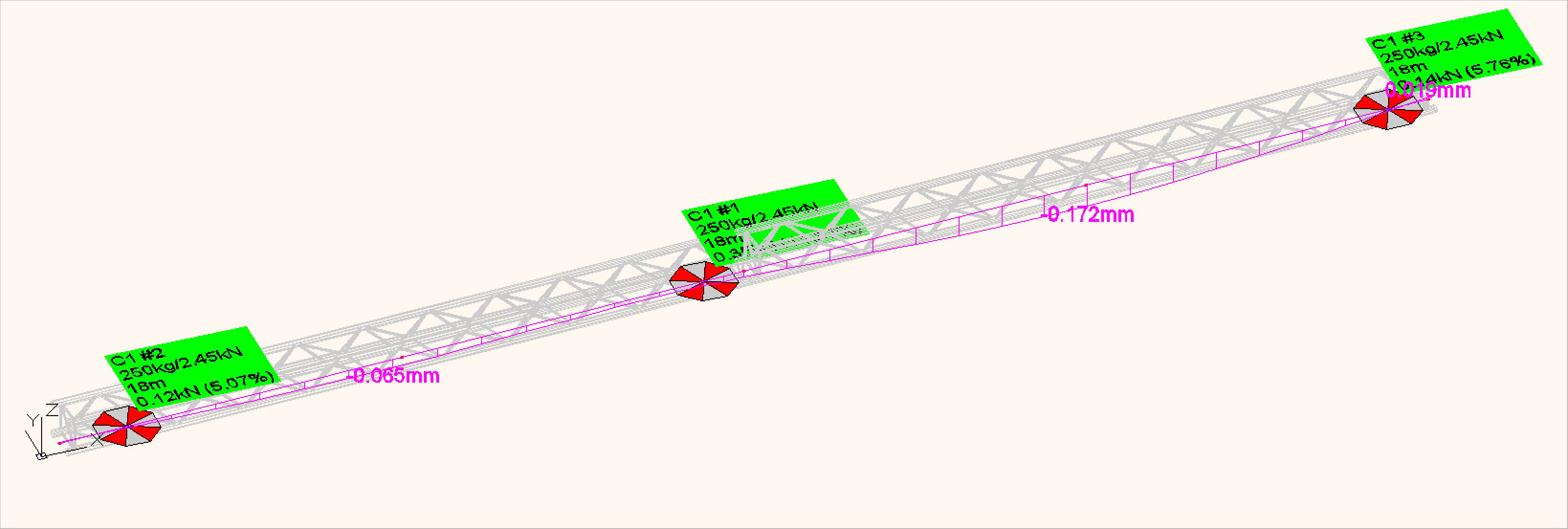 Eine Traverse mit drei Auflagern
Fall 1: Positiver Anzug in der Mitte Bis zu einem bestimmten Punkt wird die Last von den beiden äußeren Hängepunkten auf den Hängepunkt in der Mitte um verteilt. Ab dem Punkt wo der mittlere Motor die gesamte Last trägt, lässt sich das System nicht mehr nach Theorie II. Ordnung berechnen. Wenn Sie nach Theorie I. Ordnung rechnen bekommen die beiden äußeren Hängepunkte eine negative Kraft. Der Punkt an dem der mittlere Punkt die gesamte Last aufnimmt lässt sich nur durch iteratives Vorgehen bestimmen.
Fall 2: Negativer Anzug in der Mitte Die Last am mittleren Hängepunkt nimmt ab. Ab einem gewissen Punkt bekommt das Lager überhaupt keine Last mehr. Das System bleibt normal nach Theorie II. Ordnung berechenbar. Nach Theorie I. Ordnung bekommt das Lager negative Kräfte.
Fall 3: Positiver Anzug an der Seite Der mittlere Hängepunkt wird immer mehr entlastet. Die Last verteilt sich gleichmäßig auf die beiden äußeren Lager. Ab einem bestimmten Punkt fällt das Lager in der Mitte aus. Das System bleibt normal nach Theorie II. Ordnung berechenbar. Nach Theorie I. Ordnung bekommt das Lager negative Kräfte.
Fall 4: Negativer Anzug an der Seite Ab dem der Hängepunkt an der Seite der nicht herabgelassen wurde keine Last mehr bekommt ist das statische System nicht mehr berechenbar.
|